헝거포드 추상대수학 69p Q30.

문제 : Let R be a commutative ring with identity with b∈R. Let T be the subring of all multiples of b,

 T={r⋅b:r∈R}. If u is a unit in R with u∈T, prove that T=R.

 

- 다른 풀이 : https://math.stackexchange.com/questions/670369/condition-under-which-the-subring-of-multiples-of-an-element-equal-the-ring-itse

 

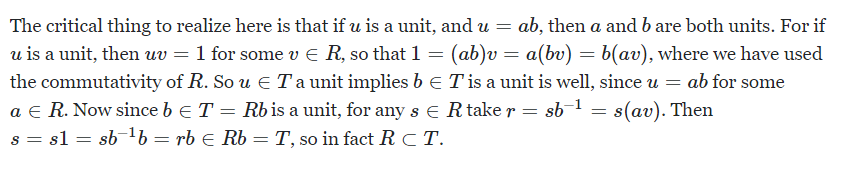
- 이 문제의 핵심은 u가 단원이므로 b도 단원인것을 알아채는것이다. (Q. 나아가 모든 T의 원소가 단원인가?)

 

- 첫문제 푸는데 너무 오래걸렸다.(대략 50분?) 전에 몇번풀어봤는데도 찾기가 어려웠다.

 

너무 멍청해진것같다. 매일 풀수는 없지만 일주일에 한번정도는 풀어볼수있지 않을까?